Using Maths to Fight Financial Crime

Financial crime has become a red-hot topic over the last 12 months, as fraudsters have sought to exploit the monitoring gaps between people, process and technology across an ever-widening attack surface – driven by the growth in usage of remote (digital) channels. Even before its recent growth, the cost of fraud and financial crime was significant. Refinitiv estimates its global cost to be more than $1 trillion annually which makes fighting it a priority for all companies, as this cost directly affects profitability.

The expanding attack surface for financial crime has increased the range of data sources required to accurately identify suspicious activity. It is no longer sufficient to focus on individual interactions, it is now critical to track the (digital) journeys that result in financial crime. That means incorporating a range of unstructured data sources into analytics - including weblogs, authentication logs and application logs - as these sources contain key information. 

It is widely acknowledged that data and analytics are key to reducing financial crime and in particular being able to correlate all relevant data. Delivering meaningful insights, however, is far from straightforward! There are a wide range of financial crime indicators across multiple domains, all of which need to be monitored in order to identify the activities that warrant further investigation.

Splunk has created a framework for accurately identifying entities (accounts, individuals or employees) that are engaged in suspicious behaviour, which is shown below. 

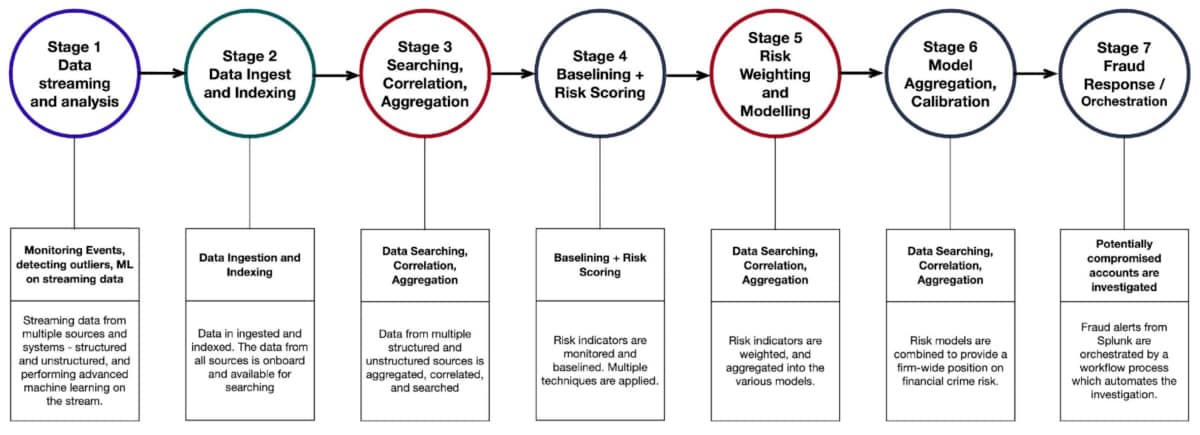
The underlying principle of this framework is that you need to be able to efficiently identify, capture and analyse data relating to each relevant risk indicator. 

But what is a risk indicator? Wikipedia defines it as a ‘risk metric used by organizations to provide an early signal of increasing risk exposure in various areas of the enterprise’. And that is exactly what our financial crime framework seeks to do – identify entities that are behaving in a way that suggests risk and therefore warrant further investigation. 

Examples of individual risk indicators could include:

• Multiple failed logins in a short time period,
• Transactions that have a significantly higher or lower value than a ‘typical’ transaction, or
• Payments made to an entity on a sanctions watchlist   

Only by looking at all risk indicators for an entity can we accurately predict which are likely to have been compromised and hence susceptible to Financial Crime.

As each risk indicator will have different importance to the organisation, this needs to be reflected in analytics. Our framework allocates a risk score to each indicator to reflect its relative impact. For example, many instances of financial crime start with account takeover. Given this, it may be that you want to allocate a higher risk score to the primary indicators of account takeover e.g multiple failed logins in a short time period.

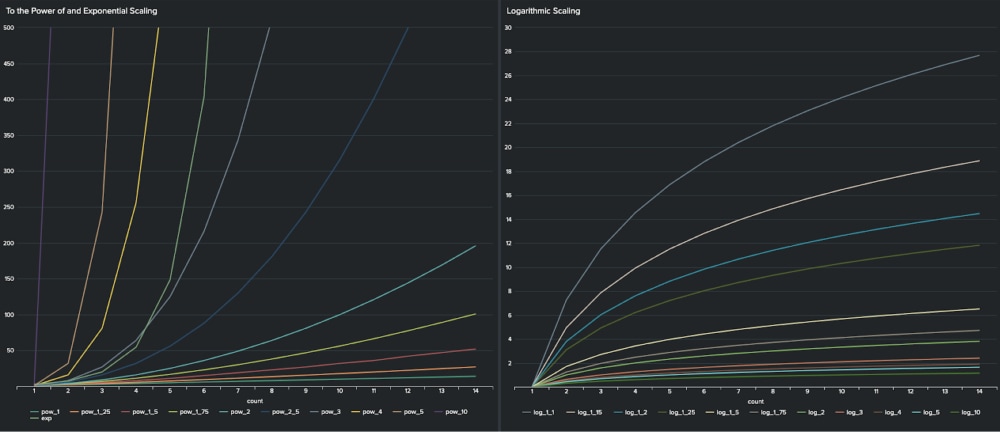
Once risk scores have been established, it is then important to think about how these should increase as data from a risk indicator gets more concerning. For example, if there is not just one failed login (which could be a typo) but two, three, four or five. In this example, there is incremental risk associated with each additional login, so the risk score for failed logins needs to increase quickly after the first failed login to reflect the way the risk manifests itself. This is where mathematics comes in, as for this indicator risk definitely increases in a non-linear way.

There are a range of non-linear mathematical curves that can be used to represent the increase in risk that an individual indicator demonstrates, some of which are outlined in the graphic below. On the left-hand side, there are a series of curves where the rate of increase accelerates (e.g squared, cubed, exponential). These will be appropriate for indicators where risk increases quickly with successive events e.g. anomalous transactions. On the right-hand side, there are a series of logarithmic curves where risk increases quickly after the first few events, but the incremental risk falls at a certain level e.g number of failed logins.

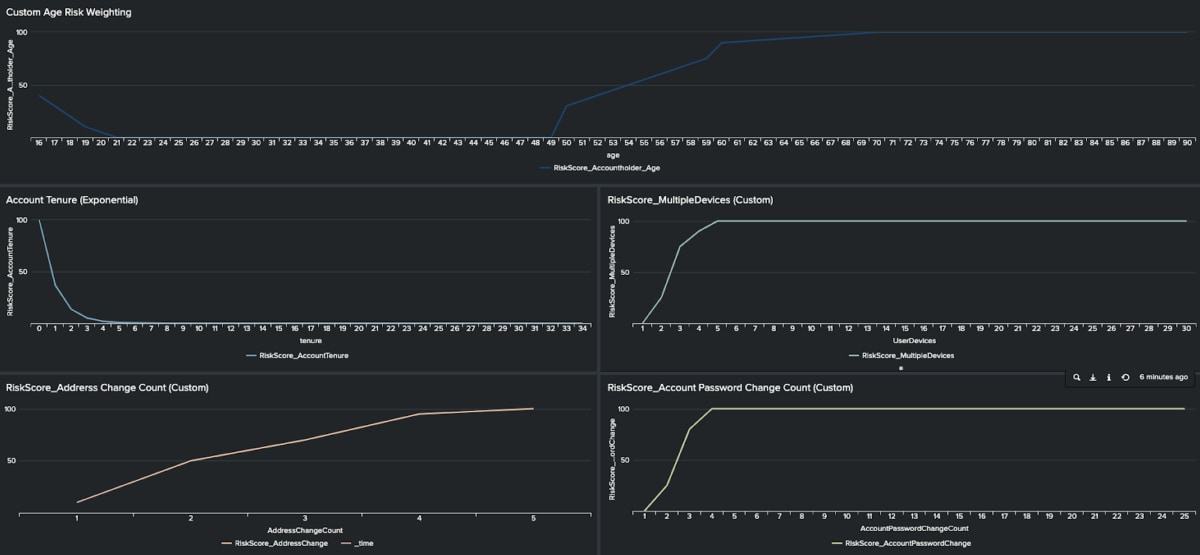
Some more tailored examples of risk scoring that we’ve applied to individual indicators are shown below. In each of these examples, we’ve modified the curve to reflect the risk associated with the specific indicator. Only by selecting the most appropriate curve for each and every risk indicator can we accurately assess the risk associated with any entity.

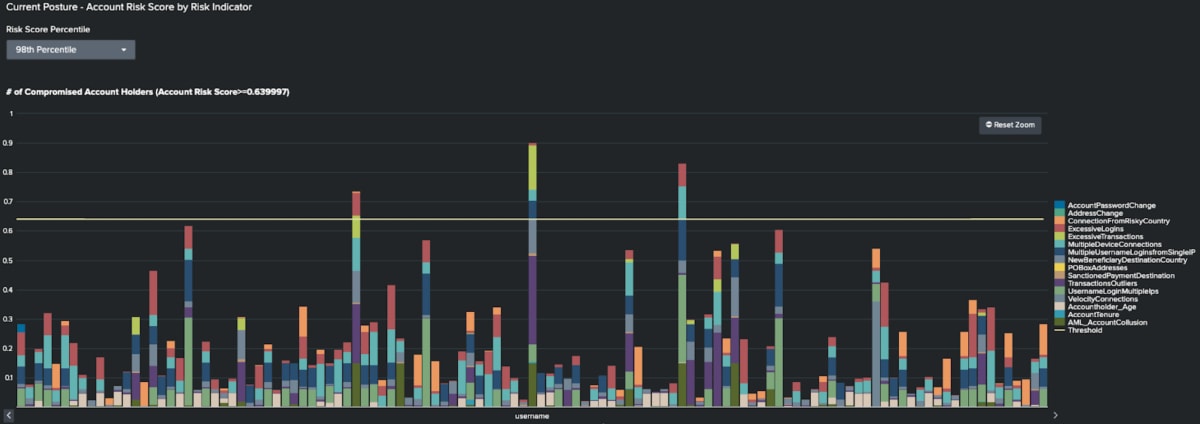
Once the process of defining all risk indicators is complete, you can calculate a cumulative risk score. It is this cumulative score that identifies the most concerning entities i.e those that warrant further investigation. Example output is shown below.

In this example, there are 15 risk indicators. The total risk score for each entity is calculated by summing the risk score across all individual indicators. Only those entities with the highest risk scores will warrant further investigation. To identify the highest priority entities for investigation, we have drawn a line at the 99^th percentile in this example. 

This approach can be applied consistently to detect financial crime in any organisation. It is very flexible and adaptive in that you only select those risk indicators relevant. You can also change both the risk indicators and the risk scoring approach whenever it is appropriate to do so e.g to reflect changes in market conditions or your risk posture.

So what are you waiting for? It’s time to reconnect with your inner maths geek and fight back!