Predicting Resource Exhaustion with Double Exponential Smoothing

A fundamental challenge in monitoring and operating cloud-native architecture is capacity planning: an undersupply of resources can lead to performance issues or outages, while an oversupply can be expensive.

In this post, we outline three methods for managing this challenge, in order of increasing accuracy and ability to handle complex data patterns: static thresholds, linear projection, and double exponential smoothing. Double exponential smoothing in the Splunk Infrastructure Monitoring toolkit of time series processing algorithms, and this use case is a primary application.

Static Thresholds

A classic task for a DevOps engineer is to monitor disk usage and alert when the resource “available disk” is running out (i.e., capacity needs to be added). This use case arises consistently among our customers.

A common approach is to trigger an alert when disk utilization goes above a certain percentage (of total disk), say 80%, for a certain duration, say 15 minutes. In SignalFlow this would be expressed as follows.

detect(when(data(‘disk.utilization’) > 80, duration(‘15m’))).publish()

While this alerting strategy is simple and interpretable, it may result in both false positives and false negatives, even for applications with a constant disk consumption rate. For example, there may be less than 20% of disk remaining, but the consumption rate is so low (e.g., because writes are small and/or infrequent) that no additional capacity is required for some time. Alternatively, there may be more than 20% of disk remaining, but the consumption rate is so high that action is required relatively soon.

Even for simple data patterns, the urgency of an alert cannot readily be expressed in terms of a static threshold. For applications with more complex disk consumption patterns, static thresholds are even more error-prone. To translate the behavior of the metric into business terms, one needs to account for the rate of consumption of a resource in addition to the amount of resource remaining.

Linear Projection

Linear projection is a common method of forecasting, namely, projecting the value of a time series at some point in the future. Given a series s and its rate of change (in units per hour, for example) r, the estimated change in n hours is n * r. Therefore the estimated value in n hours is s + n * r.

Apply this to the resource depletion context: one wants to know when the projected value is 100, say, for some n reflecting how much advance warning is required. Supposing we want 24 hours notice, we would use the following alert strategy in SignalFlow. This alert triggers when the forecasted value is greater than 100 for 15 minutes.

s = data(‘disk.utilization’)
r = s.rateofchange() * 3600 # since rate of change in units/sec
n = 24 # warning desired, in hours
forecast = s + n * r
detect(when(forecast > 100, duration(‘15m’))).publish()

Linear projection is an improvement over a static threshold, but it can be fooled by certain data patterns. For example, if the resolution of the trend is coarser than the resolution of the data, and the data exhibits some short-term fluctuations, the forecast as calculated above may fluctuate too much to remain above 100 for 15 minutes.

Here is a customer example of a metric (memory utilization) with a consistent trend. The alert was configured to trigger when the 24-hour forecast is above 100 for 20 minutes.

The host ran out of memory, but no alert was triggered. The roughly linear trend seems obvious, so we should have received an alert!

The problem is that the metric’s rate of change oscillates around zero, but this appears only upon magnification. Here is a typical segment of the above period.

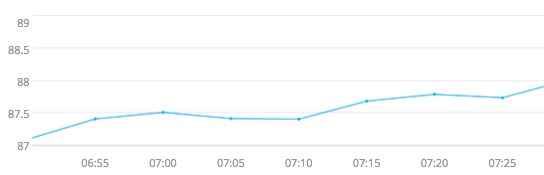
On any sufficiently large window, the increasing trend is clear. However, it is never true that for 100% of 20 minutes, the linear projections are worrisome and hence the alert was not triggered. One can relax the 100% to a smaller percentage, but it may be the case that decreases are more common than increases, but the increases are sufficiently larger than the overall trend is increasing.

This type of false negative motivated us at Splunk to find a method of forecasting trends that better handles short-term variation.

Double Exponential Smoothing

Linear projection improves on a static threshold by taking into account the trend, but the forecast may fluctuate wildly. Double exponential smoothing directly models the trend over a specified time window and consequently does not suffer from local fluctuations.

We continue with the preceding example. In the following chart, the trend is modeled on 4 hours of data (sufficiently wide to capture the consistent upward trend) and forecasted 24 hours into the future (corresponding to the desired advance warning). Many hours in advance of running out of memory, the 24-hour forecast is above 100, meaning an alert would have been triggered.

The SignalFlow is quite simple, as the complexity is contained in the internals of the "double_ewma" method.

s = data(‘memory.utilization’)
detect(when(s.double_ewma(over='4h', forecast='24h') > 100)).publish()

The original metric is shown in blue, and the 24-hour forecast is shown in green. Whereas the alert using linear projection did not trigger, the alert using double exponential smoothing would have triggered well in advance of the problem, as the green curve crosses the threshold (100) around 4:00.

Additional Details about Double Exponential Smoothing

Given a time series x₀, x₁ , x₂ ,…, double exponential smoothing models the level of the series (whose value at time t is denoted S_t) as well as its trend (denoted B_t). After initializing S₁ = x₁ and B₁ = x₁ – x₀, these quantities are updated iteratively as follows.

S_t = ⍺  x_t + (1 – ⍺ ) (S_t-1 + B_t-1)

B_t =  β (S_t – S_t-1) + (1 –  β) B_t-1

Here ⍺ and β are numbers between 0 and 1 corresponding to the degree of smoothing, with values closer to 0 corresponding to more smoothing. Now, if one wants to forecast c periods into the future, use the formula S_t+c = S_t + c B_t. SignalFlow exposes the smoothing parameters as human-understandable durations or in their raw form, with longer durations for the "over" argument corresponding to smaller smoothing parameters. The conversions of the computation window into smoothing parameters ⍺ and β, and of the forecast window into number of periods, are done automatically. As we saw in the example above, if "stream" is a data block, we can obtain the result of double exponential smoothing as follows.

stream.double_ewma(over='4h', forecast='24h').publish()

For data at 5-minute resolution, this is equivalent to the following.

stream.double_ewma(0.13, forecast='24h').publish()

A Finite Window Implementation

A property of the update rules for S_t andB_t is that the influence of a datapoint decays as time passes, but is never eliminated. As a consequence, the result of double exponential smoothing (as described) depends on the “start time” of the computation. While double exponential smoothing clearly produces a more accurate forecast in the above example, a naive implementation would suffer some deficiencies for visualization and alerting, especially for dynamic environments.

• [visualization] If the computation depends on the start time, the results may change as one zooms in and out on a chart (e.g., changing the time window from the last 4 hours to the last 12 hours).
• [alerting] If the computation depends on the start time, whether an alert is triggered can in principle depend on arbitrarily old data, and the particular moment at which the alert was configured.
   

Double exponential smoothing in Splunk Infrastructure Monitoring has a finite window and does not have these drawbacks: if one requests "stream.double_ewma(over='4h')", for example, the result depends on exactly the last 4 hours of data.

The values of the level and trend terms are what one would obtain by applying the smoothing procedure to the 4-hour window, but the updates do not require access to the full window of data. Just as one can calculate moving averages by incrementally adding and removing points as they enter and exit the moving window, one can incrementally add and remove points from the double exponentially weighted moving average. Adding a point is straightforward (use the update rules for the level and trend), but removing a point requires that some additional state be preserved (and updated appropriately during both addition and removal of points). As a consequence, double exponential smoothing is still very efficient in execution and can be used for real-time alerting even though its internals is more complex than many of the other statistical operations supported in Splunk.

The Splunk implementation also gracefully handles null values by decaying the contribution of a datapoint according to its age, not the number of datapoints that have arrived subsequent to its arrival.

Powerful Forecasting for Everyone

The metrics emitted by modern architecture exhibit complex data patterns. Forecasting trends in this context require time series models that cut through noise. At Splunk we are committed both to developing powerful models and to making them accessible to all users.

The double exponentially weighted moving average method is available not only via the SignalFlow API but also in Chart Builder and the Resource Running Out alert condition. In the Chart Builder, it is available after choosing EWMA in the Analytics (“F(x)”) pipeline.

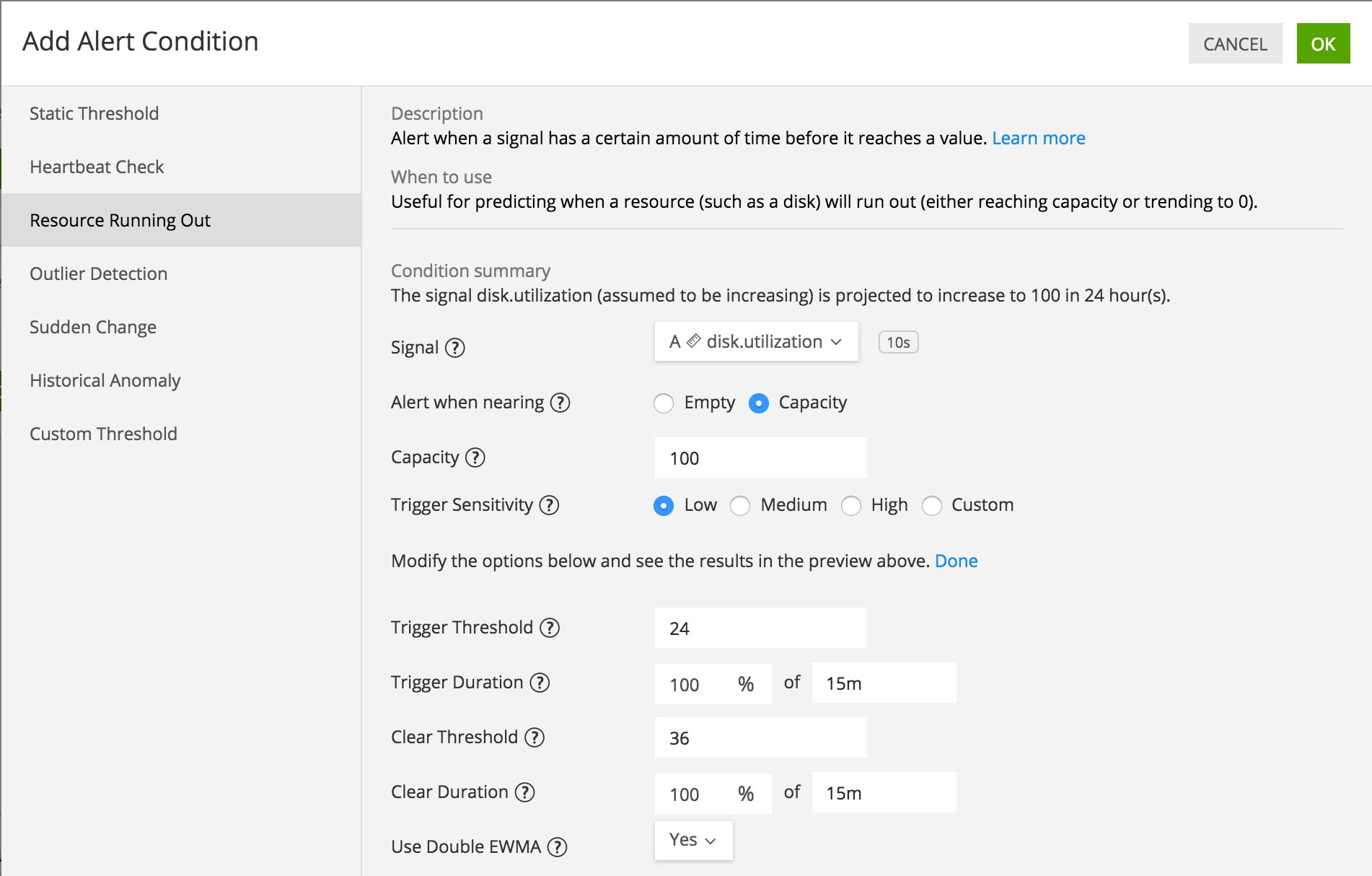
Alternatively, it is available as an argument in the Resource Running Out alert condition, as shown here. (If one selects “No” for Use Double EWMA, linear projection is used.)

Get visibility into your entire stack today with a free 14-day trial of Splunk Infrastructure Monitoring.