Real-Time Analytics with Pulsar Functions

Splunk is committed to using inclusive and unbiased language. This blog post might contain terminology that we no longer use. For more information on our updated terminology and our stance on biased language, please visit our blog post. We appreciate your understanding as we work towards making our community more inclusive for everyone.

For many event-driven applications, how quickly data can be processed, understood and reacted to is paramount. In analytics and data processing for those scenarios, calculating a precise value may be time-consuming or impractically resource intensive. In those cases having an approximate answer within a given time frame is much more valuable than waiting to calculate an exact answer. For example, to compute the exact number of unique visitors to a web page or site, you would need to keep on hand all the unique visitor records you have previously seen for comparison. Unique identifier counts are not additive either, so no amount of parallelism will help you.

If your use case does not require precise results for these types of queries, and an approximate answer is acceptable, then there are a number of techniques and algorithms that will provide you accurate approximations orders of magnitude faster and require orders of magnitude less memory. Fortunately, there are several open source libraries that provide implementations for each of the patterns discussed in this blog post, making it a relatively straight-forward process to leverage these libraries inside an Apache Pulsar Function.

Approximation Design Patterns

This category of patterns includes techniques for providing approximate values, estimates, and random data samples for statistical analysis when the event stream is either too large to store in memory or the data is moving too fast to process.

Instead of being forced to keep such a large amount of data on hand, we leverage algorithms that utilize small data structures, known as sketches, that are usually kilobytes in size. Sketches are also streaming algorithms, in that they only need to see each incoming item only once. Both these properties make these algorithms ideal candidates for deployment on edge devices.

Pattern 1: Membership

Sometimes we need to determine if we have seen a stream element in the past with a reasonable amount of certainty, without having to query an external data store. Given that we can’t keep the entire stream history in memory, we have to resort to an approximation technique that leverages a data structure known as a Bloom filter, which is a space-efficient, probabilistic data structure that is used to test whether an element is a member of a set or not.

^{Figure 1: Bloom Filter Algorithm}

As shown in Figure 1, every bloom filter uses two key elements to perform its job.

1. An array of N bits, initialized to 0
2. A collection of K independent hash functions h(x), that takes a value and generates a number that is less than N.
    

Whenever a new element is added to the filter, each of the hash functions are applied to the element. These hash values are treated as indexes into the bit array, and the corresponding array element is set to “1”.

When checking to see if an element already exists in the filter, we apply the hash functions again, but this time perform a lookup into the array for each of the hashed indexes. If at least one of these are set to zero then we know that the element DOES NOT exist in the filter. A key feature of Bloom Filters is that they are guaranteed to not return a false negative. Therefore you either know with absolute certainty that the element is NOT a member of the set, or that it MAY be in the set and will require additional logic to make that determination.

As you can see in the following example, which leverage’s Twitter’s stream-lib implementation of the Bloom Filter algorithm, the simplest use of a Bloom Filter is filtering. When a new event is processed by the Pulsar Function, it first checks to determine if we have already seen this event, and if has not, routes it to the “Not Seen” topic for further processing.

import org.apache.pulsar.functions.api.Context;
import org.apache.pulsar.functions.api.Function;
import com.clearspring.analytics.stream.membership.BloomFilter;

public class BloomFilterFunction implements Function<String, Void> {
    BloomFilter filter = new BloomFilter(20, 20);

    Void process(String input, Context context) throws Exception {
      if (!filter.isPresent(input)) {
        filter.add(input);
        // Route to “not seen” topic
        context.publish(“notSeenTopic”, input);
      }
      return null;
   }
}

Pattern 2: Event Frequency

Another common approximated statistic is the frequency at which a specific element occurs within an endless data stream with repeated elements, useful in answering questions such as, “How many times has element X occurred in the data stream?” These types of answers are particularly useful in network monitoring and analysis.

So why do we need to settle for an approximation, when calculating the sample frequency is a straightforward process? Why not just keep a count of the observations for each sample and then divide that by the total number of observations to derive the frequency?

In many high-frequency event streams there simply isn’t enough time or memory to perform these calculations. Consider trying to analyze and sample the network traffic over just a single 40 Gbps connection that can handle over 78 million 64-byte packets per second. There simply isn’t enough time to perform the calculations or store the data for just that single 40 Gbps connection, let alone a network consisting of several such network segments.

^{Figure 2: Count-Min Sketch Algorithm for Event Frequency}

In such a scenario you can choose to forego an exact answer, which will we never be able to compute in time, for an approximate answer that is within an acceptable range of accuracy. The most popular algorithm for estimating sample frequency is Count-Min Sketch, which as the name suggests, provides a sketch (approximation) of your data without actually storing the data itself. As shown in Figure 2, the Count-Min Sketch algorithm uses two elements to perform its job:

1. An M-by-K matrix of counters, each initialized to 0, where each row corresponds to a hash function
2. A collection of K independent hash functions h(x).
    

When an element is added to the sketch, each of the hash functions are applied to the element. These hash values are treated as indexes into the bit array, and the corresponding array element is incremented by 1.

Now that we have an approximate count for each element we have seen stored in the M-by-K matrix, we are able to quickly determine how many times an element X has occurred previously in the stream by simply applying each of the hash functions to the element and retrieving all of the corresponding array elements like we did upon insertion. However, this time rather than incrementing each of these array elements, we take the SMALLEST value in the list and use that as the approximate event count.

Because we never decrement a counter, this algorithm can only overestimate the event frequency. This way, we know that we have seen the element AT MOST as many times as the value returned. The accuracy of the Count-Min Sketch algorithm is controlled by the number of hash functions, k. In order to achieve a error probability of X, you need to set k >= log 1/X, which for even a modest size of k=5, results in 1% error probability.

After the input is added to the sketch, the estimated count is immediately available and can be used to perform any manner of logic based upon that count, including simple functions such as filtering events, generating alerts if the count exceeds a threshold, or more complex functions such as publishing the updated count to a external data store for display on a dashboard, etc.

import org.apache.pulsar.functions.api.Context;
import org.apache.pulsar.functions.api.Function;
import com.clearspring.analytics.stream.frequency.CountMinSketch;

public class CountMinFunction implements Function<String, Void> {
   CountMinSketch sketch = new CountMinSketch(20,20,128);

   Void process(String input, Context context) throws Exception {
      sketch.add(input, 1); // Calculates bit indexes and performs +1
      long count = sketch.estimateCount(input);
      // React to the updated count
      return null;
   }
}

Pattern 3: K-Frequency-Estimation, aka “Heavy Hitters”

Another common use of the Count-Min algorithm is maintaining lists of frequent items, commonly referred to as the “Heavy Hitters”. This design pattern retains a list of items that occur more frequently than some predefined value, e.g. the top-K list, which is simply a list of the K most common items in the data stream, e.g. the top 10 tweets on Twitter, or the 20 most popular products on Amazon.

This design pattern has several other practical applications such as detecting IP addresses that are sending abnormally large volumes of data (e.g. during a denial-of-service attack) or identifying stocks that have a large trading volume.

The K-Frequency-Estimation problem can also be solved by using the Count-Min Sketch algorithm. The logic for updating the counts is exactly the same as in the Event Frequency use case. However, there is an additional list of length K used to keep the top-K elements seen that is updated as shown in Figure 3. The logic executed when an element is added to a Top-K sketch is as follows:

• Each of the hash functions are applied to the element. These hash values are treated as indexes into the bit array, and the corresponding array element is incremented by 1.
• The event frequency for the element is calculated as done in the event frequency use case by applying each of the hash functions to the element and retrieving all of the corresponding array elements, as we did upon insertion. However, this time rather than incrementing each of these array elements, we take the SMALLEST value in the list and use that as the approximate event count.
• The calculated event frequency of this element is compared against the smallest value in the top-K elements array, and if it is LARGER, we remove the smallest value and replace it with the new element.
   

^{Figure 3: Top-K Algorithm Data Flow}

Figure 3 shows the sequence of events that occur when an element is added to the Top-K sketch. First, the k independent hashes are executed and each corresponding array entry is incremented, e.g. 98+1, etc. Next, we compute the minimum value from these updated array entries (99, 108, 312,681, and 282), which in this case is 99, and compare that to the least frequent items’ frequency count. If we have a larger number, such as we do in this example, we replace it with the incoming element.

In the following Pulsar Function code example, the StreamSummary class does all of the heavy lifting with respect to keeping the top-K list up to date, so we only need to invoke the “offer” method, which first adds the element to the Sketch, and if it is in the top-K we then route it to a priority topic for further processing.

import org.apache.pulsar.functions.api.Context;
import org.apache.pulsar.functions.api.Function;
import com.clearspring.analytics.stream.StreamSummary;

public class CountMinFunction implements Function<String, Void> {
     StreamSummary<String> summary = new StreamSummary<String> (256);

     Void process(String input, Context context) throws Exception {
        // Add the element to the sketch
        summary.offer(input, 1)
        // Grab the updated top 10,
        List<Counter<String>> topK = summary.topK(10);
        return null;
     }
}

After the input is added to the sketch, the updated Top-K is immediately available and can be used to perform any manner of logic such as publishing the updated Top-K list to a external data store for display on a dashboard, etc.

Pattern 4: Counting Distinct Elements

There are use cases where we want to count the distinct elements (e.g. IP addresses, unique web visitors, or distinct ad impressions) in a data stream with repeated elements. This is a well known problem within computer science referred to as the Count-distinct Problem. Approximation of this works well in resource-constrained environments where we cannot store the entire stream in memory and must rely on probabilistic algorithms. Currently there are two types of algorithms used to solve the count-distinct problem:

• Bit-pattern Based: The basis of these algorithms, which includes LogLog, HyperLogLog, and HyperLogLog++, is the observation that the number of distinct elements in a data stream can be estimated by calculating based upon the binary representation of each number in the set.
• Order-statistics Based: Algorithms in this category include MinCount and Bar-Yossef, which are both based on order statistics such as the smallest values that appear in the stream.
   

HyperLogLog

The basic flow of the HyperLogLog algorithm consists of the four steps shown in Figure 4, which takes the element being counted and performs a hash on it to get a hash value, which is then converted into a binary string.

The least p significant bits of the binary string are used to determine which register position will be updated. The value of p, which must be greater than zero, controls the precision of the estimate. So the higher the value of p, the more precise the estimate, but at a tradeoff of space, as each increase in p results in an exponential increase in space, i.e. the space requirement is 2^p.

Once the register position is known, the algorithm exploits a phenomenon known as “bit pattern observables”, by counting the number of zeros starting from the right for the rest of the bit string and adding one to it. This final value is then placed in the register position we determined earlier.

^{Figure 4: HyperLogLog Algorithm Data Flow}

Fortunately, there is an Apache Licensed implementation of the HyperLogLog algorithm available, which we can leverage inside the following Apache Pulsar Function:

import org.apache.pulsar.functions.api.Context;
import org.apache.pulsar.functions.api.Function;
import io.airlift.stats.cardinality.HyperLogLog;

public class HyperLogLogFunction implements Function<Integer, Void> {
   HyperLogLog hll = HyperLogLog.newInstance(2048);

   Void process(Integer value, Context context) throws Exception {
       hll.add(value);
       Integer numDistinctElements = hll.cardinality();
       // Do something with the distinct elements
   }
}

Let’s walk through the process of adding a data element to a HyperLogLog to get a better feel for what takes place. In Figure 5 below, we can see on the left hand side that the raw value we are adding is “10,529,222”. The hash value generated from the raw value, is 2,386,714,787 as shown on the right.

The binary string representation of the hash value is shown below, with the 6 least significant bits colored blue, and the remaining digits colored green. The 6 least significant bits represent the decimal value 35, which we we use as the index into the register.

Next, we start counting the number of consecutive zeros from the RIGHT most digit of the remainder and moving left, and we get exactly one. We then add 1 to that value to arrive at a value of 2, which is placed in the 35th register shown in red. This process is repeated for every element that is added.

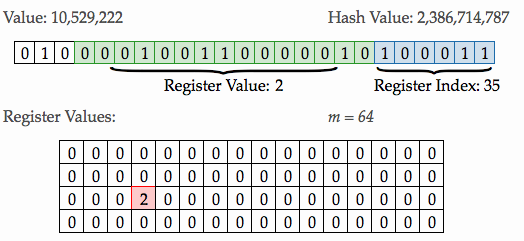
^{Figure 5: Element Processing inside the HyperLogLog Algorithm}

Conclusion

In this blog post, we covered several approximation algorithms whose space-efficiency and constant time performance make them ideal candidates for performing analysis on streaming data sets.

We took a deep dive into the real-time analytical capabilities based on probabilistic algorithms and provided several example Pulsar Functions that leverage existing open-source implementations of these algorithms to make it easy for you to get started.

The key take-away from this blog post is how easy it is to incorporate existing implementations of these complex algorithms into Apache Pulsar Functions that you can then deploy within resource-constrained environments. This allows you to take advantage of these approximation techniques without having to understand and/or code them yourself.

----------------------------------------------------
Thanks!
David Kjerrumgaard